This is the actual post for today, which continues from yesterday’s post. Today we will elaborate upon yesterday’s concepts just a little bit more.
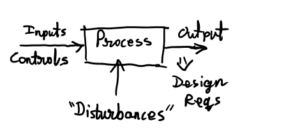
Figure 1: An overly simplified represenation of process control. New diagram coming soon.
There are two main kinds of variation–determinstic and random. Determinstic variations originate from the equipment, material, and/or operation of a unit manufacturing process.
Recall: A manufacturing process involves a change in a workpiece/material. As stated in the previous post, we can either change geometry (e.g. key dimensions or shape changes) or constitutive properties (e.g. chemical, mechanical, thermal, electrical) in the process.
Random variation is the variation that still occurs when there is no clear deterministic cause. We can model random variation using probabilistic models with statistics as outputs, and thus predict with a certain level of confidence the deviation from expected behavior. To model deterministic variations, we find causes based on process physics and first principles, creating predictive models to calibrate globally. Deterministic principles do not govern small local variations, however empirical models can be created such as via regression or curve-fitting based on determistic input that can be calibrated locally for small variations.
In statistical process control, we assume inherent randomness in a process. We then create models of this randomness to characterize this behavior and to distinguish from deterministic behavior. The models are then used to compare or improve the behavior of a process. You can look more into a general process model for control with this in mind when completing MITx 2.830.1x (retroactively edited).
Primary source (for this post and for yesterday):
D. Montgomery, Introduction to statistical quality control. Hoboken, NJ: Wiley, 2013.

